Latency
FaultTree User's Tutorial
TOCLatent Component Events
The identification of latency is perhaps one of the most valuable contributions to safety and reliability engineering. Latent component events are characterized by hidden failures (or faults) which represent conditions under which additional failures will combine to propagate system failure, or undesired events. Similar to exposure time with the non-repairable model, latent events have exposure over an interval between inspections accompanied by any needed repair. The longer the interval, the higher the probability that a latent component will be in a failed state. Scheduling and even designing a system to permit inspection, proof or validation tests becomes key to risk reduction.
An example to be studied for this topic is presented on page 24 of the DOE Handbook [for] Chemical Process Hazards Analysis.
In this study the undesired event is HF Vaporizer Rupture. The fault tree studied here will be embellished with hypothetical data and developed in a bit more detail than the milquetoast version provided in the handbook. Although not a factor in the 1992 release event at Oakridge, nor in the text of the handbook, this example study will consider the combination of rupture disk and relief valve, PRV4, in more detail.
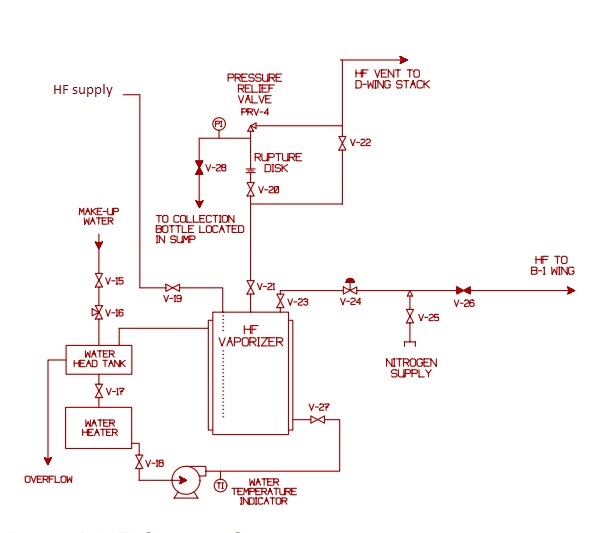
This combination of relief devices is required in such corrosive service as HF gas. If the relief valve were not isolated in this way it would be subject to corrosion due to minute leakage through the safety valve seat permitting HF vapor to contact moist ambient air. However this required feature will add risk to the performance of the pressure relief function. In particular it is somewhat likely that the rupture disk may form a pin-hole leak that will pressurize the piping inside V28, PRV4 and the rupture disk. Thus rendering the rupture disk incapable of performing its required function upon process pressure increase.
In this case latency is observed in the primary function of the relief valve, minute leakage in the rupture disk, the indication ability of the pressure gauge, and in the manual position of the isolation valves V-20 and V-21. three inspection protocols have been envisioned for this system In order to mitigate the effects of the potentially hidden flaws as follows:
rv_test
This is a rather expensive test that must be done while the system has been decommissioned, likely for other extensive maintenance. Relief valve PRV4 will be replaced with a new or reconditioned valve. The old valve will be sent out for bench test and any required reconditioning. Upon restoration of the system a pi_test and walkby will also be completed.
pi_test
This test involves applying a modest pressure of nitrogen through a connection at V28. During this test verification is made of the pressure gage integrity. It is also likely that some disposable testing device might be used to verify that no leakage of HF gas is occurring through the rupture disk. Upon completion of a pi_test a walkby will also be completed.
walk-by
This easiest test requires no intervention on the system other than possible call for remediation. The operator/inspector will log the pressure indicated on the pressure gauge and make note of the position of the isolation valves V20 and V21.
The expense of testing usually places a limit on frequency of tests. For this example it is first assumed that the rv_test is scheduled every 3 years. The pi_test is conducted annually and a monthly log is required from the operators from a walkby inspection.
Various assumptions have been made on failure occurrence for many items. No more detail has been developed for the overpressure demands than in the DOE handbook. For the latent events an input value, pzero=0, has been utilized since the undesired event is unlikely risked during conduct of testing including any required remediation. A sample fault tree is built using the following script:
rv_test=3
pi_test=1
walkby=1/12
hf<-ftree.make(type="or", name="HF Vaporizer", name2="Rupture")
hf<-addLogic(hf, at=1, type="inhibit", name="Overpressure", name2="Unrelieved")
hf<-addDemand(hf, at=1, mttf=1e6, name= "Vaporizer Rupture", name2="Due to Stress/Fatigue")
hf<-addLogic(hf, at=2, type="or", name="Pressure Relief System", name2="in Failed State")
hf<-addLogic(hf, at=2, type="or", name="Overpressure", name2="Occurs")
hf<-addLogic(hf, at=4, type="or", name="Pressure Relief", name2="Isolated")
hf<-addLatent(hf, at=6, mttf=10, pzero=0, inspect=walkby, name="Valve 20", name2="Left Closed")
hf<-addLatent(hf, at=6, mttf=10, pzero=0, inspect=walkby, display_under=7,
name="Valve 21", name2="Left Closed")
hf<-addLogic(hf, at=4, type="or", name="Rupture Disk Fails", name2="to Open at Design Pt.")
hf<-addLogic(hf, at=9, type="or", name="Installation/Mfr", name2="Errors")
hf<-addProbability(hf, at=10, prob=.001, name="Rupture Disk", name2="Installed Upside Down")
hf<-addProbability(hf, at=10, prob=.001, display_under=11,
name="Wrong Rupture Disk", name2="Installed")
hf<-addProbability(hf, at=10, prob=.001, display_under=12,
name="Rupture Disk", name2="Manuf. Error")
hf<-addLogic(hf, at=9, type="or", name="Pressure Between Disk", name2="and Relief Valve")
hf<-addLogic(hf, at=14, type="inhibit", name="Pressure NOT" , name2="Detectable by PI")
hf<-addLatent(hf, at=15, mttf=10, pzero=0, inspect=pi_test,
name="Pressure Gage", name2="Failed Low Position")
hf<-addLatent(hf, at=15, mttf=10, pzero=0, inspect=pi_test,
name="Rupture Disk Leak", name2="Undetected")
hf<-addLogic(hf, at=14, type="inhibit", name="Pressure" , name2="Detectable by PI")
hf<-addProbability(hf, at=18, prob=1-4.8374e-2, name="Pressure Gage", name2="Detects Pressure")
hf<-addLatent(hf, at=18, mttf=10, pzero=0, inspect=walkby,
name="Rupture Disk Leak", name2="Detectable")
hf<-addLogic(hf, at=4, type="or", name="Pressure Relief Fails", name2=" to Open at Design Pt")
hf<-addLatent(hf, at=21, mttf=300, pzero=0, inspect=rv_test,
name="Pressure Relief", name2="set too high")
hf<-addLatent(hf, at=21, mttf=300, pzero=0, inspect=rv_test,
name="Pressure Relief Unable", name2="to Open at Design Pt")
hf<-addDemand(hf, at=5, mttf=10, name= "High Pressure", name2="Feed to Vaporizer")
hf<-addDemand(hf, at=5, mttf=10, name= "Vaporizer Heating", name2="Runaway")
The fault tree is calculated then prepared for view in the browser:
hf<-ftree.calc(hf)
ftree2html(hf, write_file=TRUE)
browseURL("hf.html")
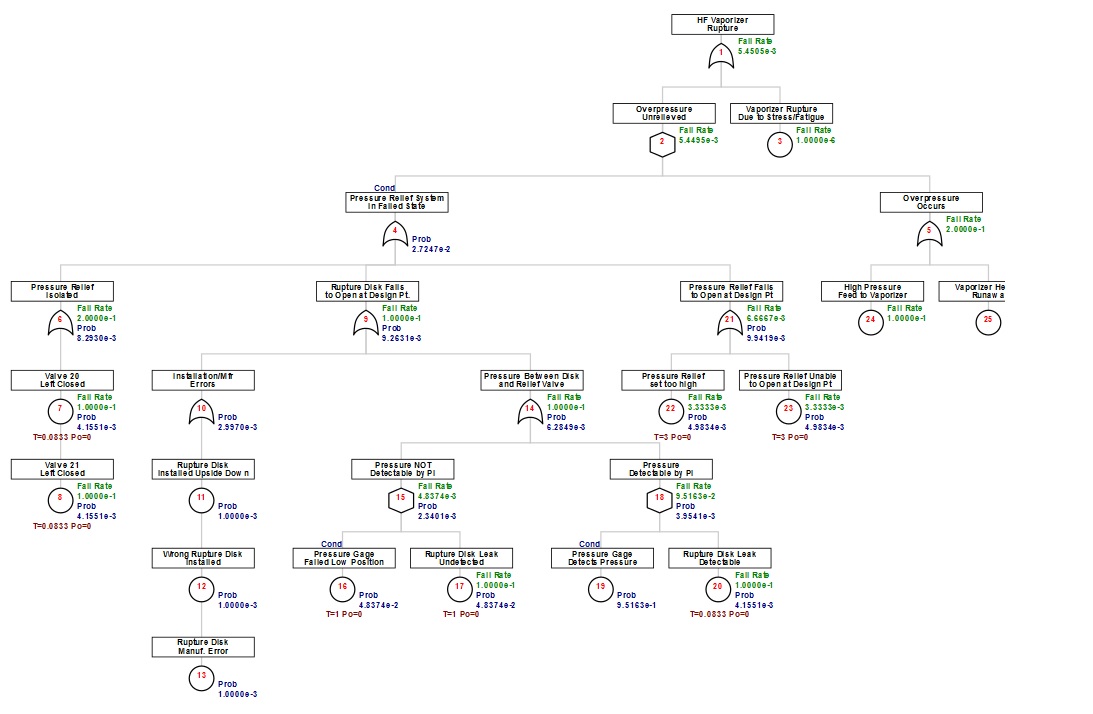
In this example the occurrence of the undesired event, HF vaporizer rupture, is so severe that restoration of the pressure relief system from its failed state is irrelevant. This is a condition that presents only a probability to an inhibit gate for combination with the overpressure demands. Demands are typically events that can have devastating effect, but insignificant duration. Like lightning striking.
Under the OR gate at node 14 two inhibit gates are used to distinguish two complimentary conditions. The condition at node 15 is failure of pressure gauge in such a manner that pressure between the rupture disk and relief valve would not be detected. This state also alters the nature of the latent failure of a pin-hole leak in the rupture disk because its detection interval now depends on the pi_test. Node 18 has a complimentary probability for when the pressure gauge is not in a failed state. One way to place an accurate probability at the event at node 19 is to first calculate the tree (with a probability of 1 at node 19) to determine the probability of node 16 to be subtract from 1. This is an example of splitting probability of time by INHIBIT gates that then get combined by an OR. In this case the probability at node 16 is so small that a probability of 1 could have been used at node 19 without significant loss of accuracy on the overall tree calculation. Although the portion of time that the pressure gauge is not functional is small, this condition can add a significant probability that the rupture disk functionality will be compromised.
The key impact of latency is in the calculation of the probability of the failed state for the event. Similar to exposure time, the event may occur anywhere within the interval between inspections. The exact time of failure is unknown, however using the exponential function for the assumption of random failures, the most likely time of failure can be calculated. The probability of failed state is then assumed to occur from that point forward. This is called the fractional downtime calculation. The function used to determine this probability is dependent on the fail rate (1/mttf) and inspection interval (T) as follows:
1-1/((1/mttf)*T)*(1-exp(-(1/mttf)*T))
In some systems the time required to repair or restore the failure after detection must still be accounted for as unavailable time. In other cases, there is a lingering probability that the component will still be failed after restoration. These, often small, probability values are additive to the latency probability calculation. The addLatent function has a pzero argument for assignment of this additional probability.
Using the R Environment to Alter Inspection Intervals
The resulting calculations suggest the undesired event may be expected to occur once in about 180 years. This might sound quite remote, but considering the hazards to personnel it is likely to be found unacceptable in most studies.
It is possible to alter the inspection intervals and view several fault trees to see how changes to inspection scheduling could impact the frequency of the undesired event. However, it is somewhat cumbersome to go through all those motions just to view one number at the top. Since this model is built within the R environment it is possible to program several cases and report the final result, perhaps converted to MTTF rather than very small fail rates in scientific notation. This is something I doubt will be found available in most other GUI based fault tree software
A set of test cases is constructed by combining vectors of each test parameter into a single matrix:
rv_test<-c(3,3,3,2,1,2,1)
pi_test<-c(3,1,1/12,1/12,1/12,1/52,1/52)
walkby<-c(3,1/12,1/52,1/52,1/52,1/52,1/52)
cases<-cbind(rv_test,pi_test,walkby)
This matrix can be viewed by just re-typing its name in the R Console:
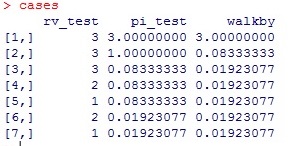
Here the original example is represented by the values in case 2. Case 1 will represent the effect of not conducting the pi_test or walkby any more frequently than the rv_test. A series of more frequent testing is sampled to get an idea of each effect. Any number of cases could be modeled in this way. With the cases matrix defined in the current R session it is possible to program a loop to build an mttf column summarizing the results of calculated fault trees for each case.
Since the probability at node 16 will be altered during various runs through the loop, unless we can alter the probability at node 18 programmatically a small inaccuracy may be entered. This is possible to accomplish in this fault tree since the latent probability of failure is calculated upon execution of the addLatent function. This code looks up this value for the proper subtraction to make the probability at node 18 complimentary to node 16 on each pass of fault tree construction.
mttf<-NULL
CFRat14<-NULL
for(case in 1:dim(cases)[1]) {
rv_test<-cases[case,1]
pi_test<-cases[case,2]
walkby<-cases[case,3]
hf<-ftree.make(type="or", name="HF Vaporizer", name2="Rupture")
hf<-addLogic(hf, at=1, type="inhibit", name="Overpressure", name2="Unrelieved")
hf<-addDemand(hf, at=1, mttf=1e6, name= "Vaporizer Rupture", name2="Due to Stress/Fatigue")
hf<-addLogic(hf, at=2, type="or", name="Pressure Relief System", name2="in Failed State")
hf<-addLogic(hf, at=2, type="or", name="Overpressure", name2="Occurs")
hf<-addLogic(hf, at=4, type="or", name="Pressure Relief", name2="Isolated")
hf<-addLatent(hf, at=6, mttf=10, pzero=0, inspect=walkby,
name="Valve 20", name2="Left Closed")
hf<-addLatent(hf, at=6, mttf=10, pzero=0, inspect=walkby, display_under=7,
name="Valve 21", name2="Left Closed")
hf<-addLogic(hf, at=4, type="or", name="Rupture Disk Fails", name2="to Open at Design Pt.")
hf<-addLogic(hf, at=9, type="or", name="Installation/Mfr", name2="Errors")
hf<-addProbability(hf, at=10, prob=.001, name="Rupture Disk", name2="Installed Upside Down")
hf<-addProbability(hf, at=10, prob=.001, display_under=11,
name="Wrong Rupture Disk", name2="Installed")
hf<-addProbability(hf, at=10, prob=.001, display_under=12,
name="Rupture Disk", name2="Manuf. Error")
hf<-addLogic(hf, at=9, type="or", name="Pressure Between Disk", name2="and Relief Valve")
hf<-addLogic(hf, at=14, type="inhibit", name="Pressure NOT" , name2="Detectable by PI")
hf<-addLatent(hf, at=15, mttf=10, pzero=0, inspect=pi_test,
name="Pressure Gage", name2="Failed Low Position")
hf<-addLatent(hf, at=15, mttf=10, pzero=0, inspect=pi_test,
name="Rupture Disk Leak", name2="Undetected")
hf<-addLogic(hf, at=14, type="inhibit", name="Pressure" , name2="Detectable by PI")
hf<-addProbability(hf, at=18, prob=(1-hf$PBF[16]),
name="Pressure Gage", name2="Detects Pressure")
hf<-addLatent(hf, at=18, mttf=10, pzero=0, inspect=walkby,
name="Rupture Disk Leak", name2="Detectable")
hf<-addLogic(hf, at=4, type="or",
name="Pressure Relief Fails", name2=" to Open at Design Pt")
hf<-addLatent(hf, at=21, mttf=300, pzero=0, inspect=rv_test,
name="Pressure Relief", name2="set too high")
hf<-addLatent(hf, at=21, mttf=300, pzero=0, inspect=rv_test,
name="Pressure Relief Unable", name2="to Open at Design Pt")
hf<-addDemand(hf, at=5, mttf=10, name= "High Pressure", name2="Feed to Vaporizer")
hf<-addDemand(hf, at=5, mttf=10, name= "Vaporizer Heating", name2="Runaway")
hf<-ftree.calc(hf)
mttf<-c(mttf,1/ hf$CFR[1])
CFRat14<-c(CFRat14, hf$CFR[14])
}
cases<-cbind(cases, mttf, CFRat14)
In order to verify that the complimentary probability has been appropriately applied at node19 a column of fail rates derived at node 14 is also prepared. This check column should always contain the basic fail rate provided for the rupture disk leak if probabilities at nodes 16 and 18 are indeed complimentary. After one or two blinks of an eye, re-typing the cases matrix name in the R Console reveals the tabularized results:
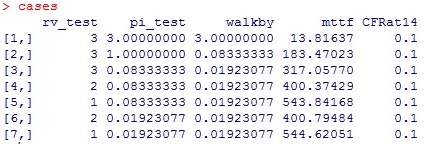
As expected, the risk of the undesired event can be impacted by judicious testing, inspection and remediation. By fault tree modeling with an understanding of latency it is possible to define an appropriate inspection protocol.
It is left as a student exercise to consider daily walkby inspections.
What inspections could be considered for the rupture disk human error and manufacturing risks?
Could replacement of the disk with a new one change these risks?
TOC
